对回文积问题的困惑

您正在测试999*(999…100),然后是998*(999…100)

因此,您将在测试997*996之前测试999*500。

首先注意乘法是反射的,a*b==b*a,所以b不需要每次从999…0开始,只要a…0。

在循环内部,如果(a+b)始终小于保存的和,则放弃内部循环并移动到下一个a。当a低于sum/2时,你找不到比你已经找到的值更高的未来值,所以你就完了。

问题是你可能会找到一个 a 999和 b 200,但你打破太快,所以你从来没有看到有一个998*997(只是例子数字)。

你需要寻找所有的回文,或者一旦你找到第一个,设置它 作为你的最低限度,继续通过 一 循环。

关于第二个问题,我的建议是以更实用的方式而不是程序性的方式来处理这个问题。因此,您可以尝试从功能上“描述”您的问题,而不是循环,让Ruby来完成这项工作:

• 从所有3位数的数字中,
  • select
    • 找到产品最大的那个

尽管这种方法可能不会产生最有效的解决方案,但它可能会教您一些Ruby习惯用法。

考虑P的数字,让它们是x,y和z。P必须至少为6位,因为回文111111=143777是两个3位整数的乘积。因为P是回文的:

P=100000x + 10000y + 1000z + 100z + 10y + x
P=100001x + 10010y + 1100z
P=11(9091x + 910y + 100z)

C#实施:

using System;

namespace HighestPalindrome
{
    class Program
    {
        static void Main(string[] args)
        {
            int i, j;
            int m = 1;
            bool flag = false;

            while (true)
            {
                if (flag) j = m + 1;
                else j = m;

                for (i = m; i > 0; i--)
                {
                    Console.WriteLine("{0} * {1} = {2}", 1000 - i, 1000 - j, (1000 - i) * (1000 - j));
                    j++;

                    //--- Palindrome Check ------------------------------

                    int number, temp, remainder, sum = 0;
                    number = temp = (1000 - i) * (1000 - j);

                    while (number > 0)
                    {
                        remainder = number % 10;
                        number /= 10;
                        sum = sum * 10 + remainder;
                    }

                    if (sum == temp)
                    {
                        Console.WriteLine("Highest Palindrome Number is - {0} * {1} = {2}", 1000 - i, 1000 - j, temp);
                        Console.ReadKey();
                        return;
                    }

                    //---------------------------------------------------
                }

                if (flag)
                    m++;
                flag = !flag;
            }

        }
    }
}

错误是你假设如果你发现回文 a 它会给你带来最好的产品,这不是真的。解决办法是保持 max_product

我可以回答你的第一个问题:你需要找到最高的产品,而不是含有最高因子的产品。换句话说 a * b 可能大于 c * d 即使 c > a > b .

最主要的是检查所有可能的值。当你找到第一个答案时,不要试图打断,只要从最佳答案0开始,然后尝试所有的组合,并不断更新最佳答案。第二件事是尽量减少“所有组合”的集合。

您可以做的一件事是将内部循环的值限制为小于或等于a(因为 b==b

for a in range.to_a.reverse do
    for b in (100..a).to_a.reverse do

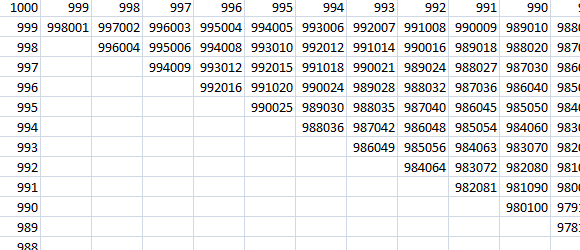
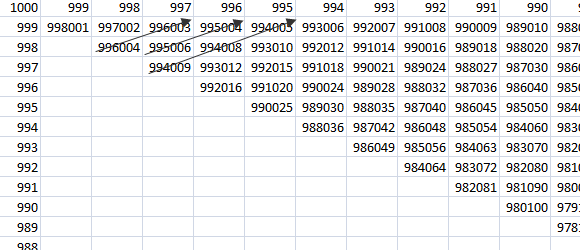
下一件事你可以做的是打破内部循环时,产品是低于当前最佳值。

c = a*b
next if c < best

下一步,如果你打算把它们都翻一遍,那么反过来翻一遍也没有什么好处。从范围的顶端开始,你需要一段时间才能找到一个回文数,因此,你需要一段时间来减少你的搜索集。如果你从底部开始,你开始迅速增加下限。

for a in range.to_a do
    for b in (100..a).to_a do

我的测试显示,无论哪种方式,你尝试一些405K对然而。那么换个角度来思考这个问题怎么样。两个三位数的最大乘积是多少?999*999=998001,最小为100*100=10000。不如我们接受你的想法,打破第一个答案,但适用于不同的范围,即998001至10000(或999*999至100*100)。

for c in (10000...998001).to_a.reverse do

我们只经过202次测试就得到了回文。。。问题是它不是两个3位数的乘积。所以现在我们要检查我们找到的回文是否是2个3位数的乘积。一旦我们在回文和两个3位数的乘积的范围内找到一个值,我们就完成了。我的测试表明,在不到93K的测试之后,我们找到了满足要求的最高回文。但是由于我们有检查所有回文是否都是两个3位数的乘积的开销,所以它可能不会比以前的解决方案更有效。

所以让我们回到最初的改进。

由于产品的对角线越来越小,你可以停止只要你找到一个palindome数字对角线。这是一个非常有效的解决方案,但实现更加复杂。结果表明,这种方法在超过2200次尝试后找到最高回文数。

ar=[]
limit = 100..999
for a in limit.to_a.reverse do
  for b in (100..a).to_a.reverse do
    c=a*b
    if c.to_s == c.to_s.reverse
      palndrm=c 
      ar << palndrm
    end  
  end
end
print ar
print"\n"
puts ar.max
puts ar.min 

实现:

max = 100.upto(999).inject([-1,0,0]) do |m, a|
  a.upto(999) do |b|
    prod = a * b
    m = [prod, a, b] if prod.to_s == prod.to_s.reverse and prod > m[0]
  end
  m
end
puts "%d = %d * %d" % max

906609 = 913 * 993

以下是我在Ruby中得出的结论:

def largest_palindrome_product(digits)
  largest, upper, lower = 0, 10**digits - 1, 10**(digits - 1)

  for i in upper.downto(lower) do
    for j in i.downto(lower) do
      product = i * j
      largest = product if product > largest && palindrome?(product)
    end
  end
  largest
end

def palindrome?(input)
  chars = input.to_s.chars
  for i in 0..(chars.size - 1) do
    return false if chars[i] != chars[chars.size - i - 1]
  end
  true
end

不过,我想可能还有更有效的解决办法。

对于这个问题,当我们在寻找最高回文时,我假设它会以9开头。因此以9结尾(回文)。

如果你注意,要得到一个以9结尾的数字,你只能得到以9和1,3和3,7和7结尾的数字。

然后检查其他值(例如999*998,因为它不会以9结尾)是没有用的。

从999和991开始,你可以把10减到991,试试999和981等等。。。 你对993和993也一样。。。993 * 983 你不需要超过900或10^4-10^3,因为你可以确定最高点会在之前。

int PB4_firstTry(int size)
{
    int nb1 = (int)pow(10.0,size+1.0) - 1, nb2 = (int)pow(10.0,size+1.0) - 1;
    int pal91 = getFirstPalindrome(size,9,1);
    int pal33 = getFirstPalindrome(size,3,3);
    int pal77 = getFirstPalindrome(size,7,7);

    int bigger1 = (pal91 > pal33) ? pal91 : pal33;
    return (bigger1 > pal77) ? bigger1 : pal77;
}

int getFirstPalindrome(int size,int ending1,int ending2)
{
    int st1 =  (int)pow(10.0,size+1.0) - 10 + ending1;
    int comp = st1 - pow(10.0,size);
    int st2 =  (int)pow(10.0,size+1.0) - 10 + ending2;
    int answer = -1;
    while (st1 > comp)
    {
        for (int i = st2; i > comp && st1*i > answer; i-=10)
        {
            if (PB4_isPalindrome(st1*i))
                answer = st1*i;
        }
        st1 -= 10;
    }
    return answer;
}

bool PB4_isPalindrome(int number)
{
    std::string str = intToString(number);
    for (int i = 0; i < (int)(str.length() / 2); i++)
    {
        if (str[i] != str[str.length() - 1 - i])
            return false;
    }
    return true;
}

std::string intToString(int number)
{
    std::ostringstream convert;
    convert << number;
    return convert.str();
}