缓存理论[关闭]

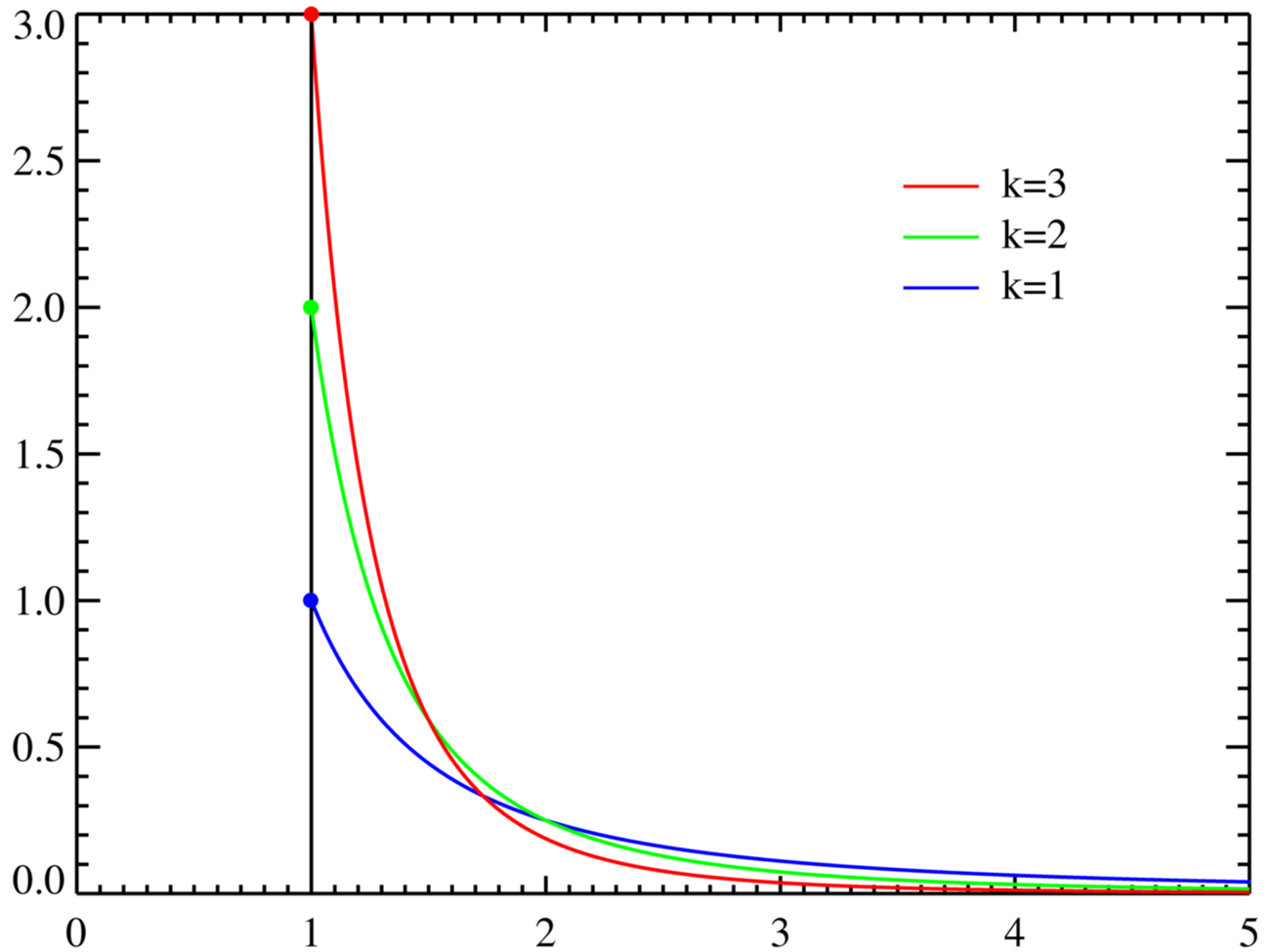
绝大多数真实缓存都涉及到利用“80-20规则”或 Pareto distribution . 下面是它的外观

这在应用程序中表现为:

• 大部分运行时都花在同一段代码中(使CPU上的代码缓存有效)
• 通常,当一个变量被访问时,它很快就会被再次访问(使CPU上的数据缓存有效)
• 当浏览器查找一次网站的主机名时,它将在不久的将来频繁地访问它(使dns缓存有效)

因此,我要说的是“缓存理论”是只使用一些额外的资源,这些资源通常是“稀有”但“快速”的,以补偿您将要执行的最活跃的重复操作。

你这样做的原因是试图根据上面高度倾斜的图表来“调整”你执行“慢速”操作的次数。

我和我学校的一位教授谈过,他指给我看 online algorithms , 这似乎是我要找的话题。

缓存算法和页面替换算法之间有很多重叠。我可能会为这些主题编辑维基百科页面,以澄清连接,一旦我 对这门学科有了更多的了解。

如果你可以假设缓存命中比缓存错误快得多,你会发现超时,即使你只有缓存缺失,使用缓存仍然比不使用缓存快或快。

数学见下文:

Number of hits = NumRequests - #CacheMisses

AverageTime = ((NumRequests-#CacheMisses) * TimePerHit + #CacheMisses * TimePerMiss)/NumRequests

如果我们假设NoMeDebug是无穷大的(这是一个极限问题,不要害怕微积分),我们可以看到:

AverageTime = Infinity*TimePerHit/Infinity - #CacheMisses*TimePerHit/Infinity + #CacheMisses*TimePerMiss/Infinity

缓存未命中的两个项都归零,但整个方程解析为:

AverageTime = TimePerHit

当然,这是因为请求的数量是无穷大的,但是您可以看到这将如何通过使用缓存轻松地加快您的系统。